เมื่อคานรับน้ำหนักแล้ว พฤติกกรมของคานจะแอ่น ผิวล่างเกิดแรงดึงจะใช้เหล็กเส้นเป็นตัวรับแรง ส่วนผิวบนเกิดแรงอัดจะใช้คอนกรีตเป็นตัวรับแรง โดยมาตรฐานการออกแบบทั่วไปจะมีข้อสมมุติฐานสำหรับการวิเคราะห์และออกแบบดังนี้

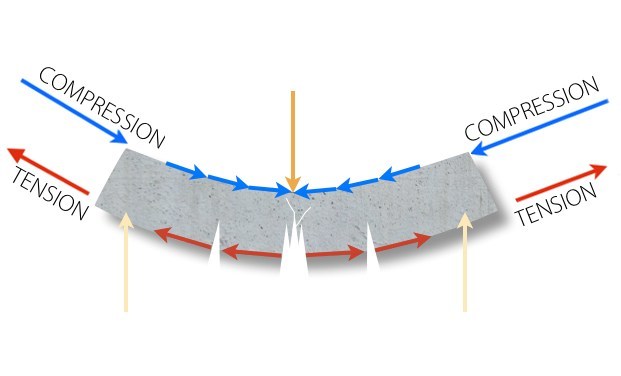
รูปที่ 1 พฤติกรรมการรับแรงอัดและแรงดึงของคานเมื่อรับแรงตามแนวดิ่ง

สมมุติฐานการวิเคราะห์และออกแบบคาน คสล. ด้วยวิธีกำลัง

• ระนาบของหน้าตัดก่อนและหลังการดัดยังคงเป็นระนาบเดียวกันไม่เปลี่ยนแปลง
• คอนกรีตรับแรงดึงได้น้อยมาก
• คอนกรีตและเหล็กยึดเกาะกันดีมาก
• หน้าตัดคอนกรีตเสริมเหล็กจะถือว่าวิบัติเมื่อความเครียดของคอนกรีต $\varepsilon_{cu} = 0.003 mm./mm.$
• หน่วยแรงอัดในคอนกรีตซึ่งไม่เป็นเชิงเส้น สามารถใช้การกระจายเป็นเชิงเส้นได้

• ความสัมพันธ์ของ Stress และ Strain ของเหล็กเสริมสามาถแบ่งได้เป็น 2 กรณี ได้แก่
  กรณีที่ 1 เหล็กเสริมไม่คราก $\varepsilon_{s} < \varepsilon_{y}$ จะได้ $f_s = E_s\varepsilon_{s}$
  กรณีที่ 2 เหล็กเสริมคราก $\varepsilon_{s} \geq \varepsilon_{y}$ จะได้ $f_s = f_y$

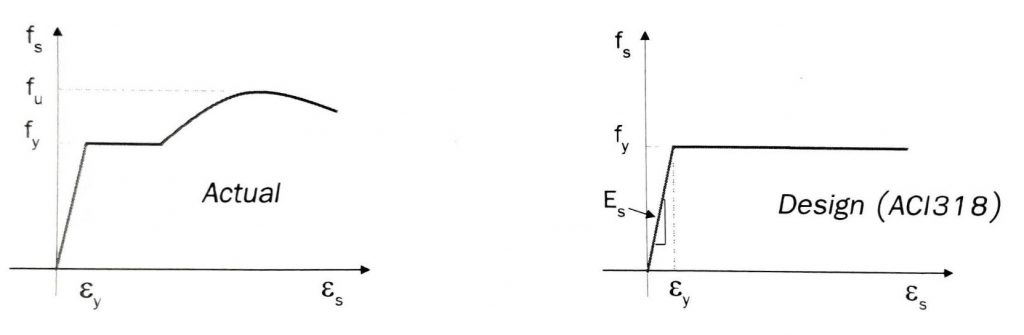
รูปที่ 2 ความสัมพันธ์ของ Stress และ Strain ของเหล็กเสริม

• ใช้โมเมนต์ความโค้ง (Moment-Curvature Relaionship, $M-\varPhi Diagram$) เป็นตัวแทนมนการพิจารณา แรงกระทำและการเคลื่อนตัวขององค์อาคาร
  โดยที่ $\varphi = \varepsilon_c/kd$ หรือ $\varphi = \varepsilon_s/(d-kd)$ และ $M=T \times jd$

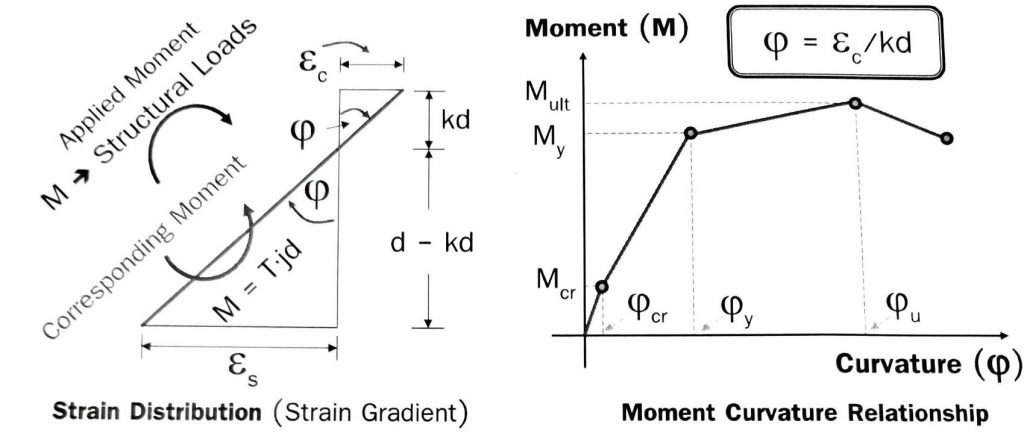
รูปที่ 3 Strain Distribution และ Moment Curvature Relationship

จากกราฟรูปที่ 3 ด้านซ้าย ถ้าอธิบายง่าย ๆ คือ ค่า Curvature ($\varphi$) จะสูงขึ้นเมื่อเหล็กยืดมากขึ้น (ความเครียดของเหล็กเพิ่ม, $\varepsilon_s$ มีค่าเพิ่มขึ้น) และพร้อมๆกันนั้น คอนกรีตก็จะถูกบีบให้หดตัวลง (ความเครียดของคอนกรีตเพิ่ม, $\varepsilon_c$ มีค่าเพิ่มขึ้น) ซึ่งพฤติกรรมนี้ จะทำให้คอนกรีตแอ่นและเกิดรอยร้าวแต่คานจะไม่วิบัติ และสามารถต้านทานโมเมนต์ได้มากขึ้นตามกราฟรูปขวา และคานจะวิบัติเมื่อความเครียดของคอนกรีตมีค่าถึงขีดจำกัด ( $\varepsilon_c = 0.003 mm./mm.$ )

สำหรับคานเปราะคือ เหล็กเส้นมีจำนวนมากเกินไป เมื่อมีแรงมากระทำเหล็กยืดตัวน้อยมาก (ความเครียดของเหล็กเพิ่มน้อยมาก, $\varepsilon_s$ เพิ่มขึ้นน้อยมาก) ส่งผลให้ Curvature ($\varphi$) น้อย คานยังไม่ทันแอ่นหรือเกิดรอยร้าว ความเครียดของคอนกรีตก็ถึงขีดจำกัดจนคานวิบัติไปเสียก่อน ($\varepsilon_c = 0.003 mm./mm$ )

พฤติกรรมของคานต่อปริมาณเหล็กเสริม

เมื่อพิจารณา Moment-Curvature Relationship ของหน้าตัดคานที่มีปริมาณเหล็กเสริมที่แตกต่างกัน จากรูปที่ 4 จะพบพฤติกรรมดังนี้

หากปริมาณเหล็กเสริมมากคานจะรับ Moment ได้มาก แต่มีค่า Curvature ต่ำ ซึ่งหมายความว่าคานวิบัติในขณะที่แอ่นตัวน้อย

เมื่อคานแอ่นตัวน้อยก็จะไม่แสดงรอยร้าวให้เห็นก่อนวิบัติ ซึ่งจะเป็นการวิบัติอย่างฉับพลัน ไม่มีรอยร้าวเตือนล้วงหน้า ทำให้ผู้อาศัยไม่สามารถอพยพได้ทัน พฤติกรรมแบบนี้เรียกว่า คานวิบัติแบบเปราะ หรือภาษาที่วิศวกรโยธาใช้คือ การวิบัติเนื่องจากแรงอัดเป็นหลัก (Compression failure)

หากคานมีเหล็กเสริมน้อย จะเห็นว่าคานสามารถต้านทาน Moment ได้น้อย แต่มีค่า Curvature สูง ซึ่งหมายความว่าคานแอ่นตัวมากก่อนจะวิบัติ ในกรณีนี้คานจะแอ่นและเกิดรอยร้าวเตือนให้ผู้อาศัยอพยพหนีได้ก่อน วิศวกรโยธาเรียกการวิบัติแบบนี้ว่า การวิบัติเนื่องจากแรงดึงเป็นหลัก (Tension failure)

แต่ถ้าอัตราส่วนการเสริมเหล็กเท่ากับ $\rho_b$ จะเป็นจุดกึ่งกลางพอดีระหว่างการวิบัติเนื่องจากแรงอัดและแรงดึง ซึ่งเรียกว่า การวิบัติที่จุดสมดุล

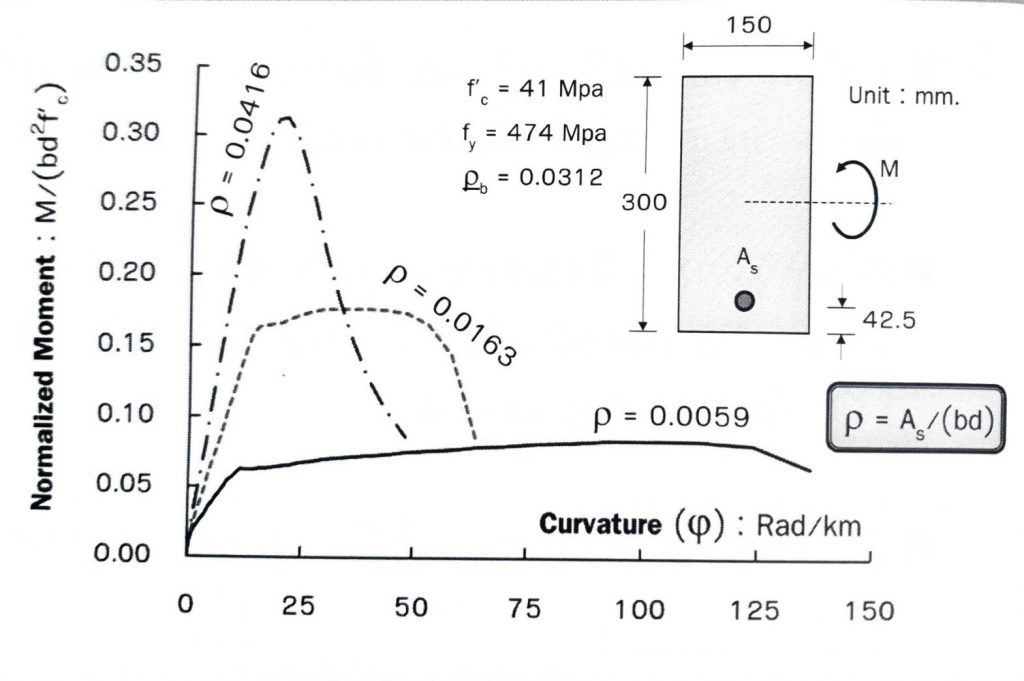
รูปที่ 4 Moment-Curvature Relationship ของหน้าตัดคานที่มีปริมาณเหล็กเสริมที่แตกต่างกัน

จากสมมุติฐานการออกแบบ จะถือว่าคานคอนกรีตเสริมเหล็กวิบัติเมื่อความเครียดของคอนกรีต $\varepsilon_{cu} = 0.003 mm./mm.$ จะได้ความสัมพันธ์ของ Strain ต่อความสูงหน้าตัดคานของแต่ละ mode การวิบัติ ดังแสดงในรูปที่ 5

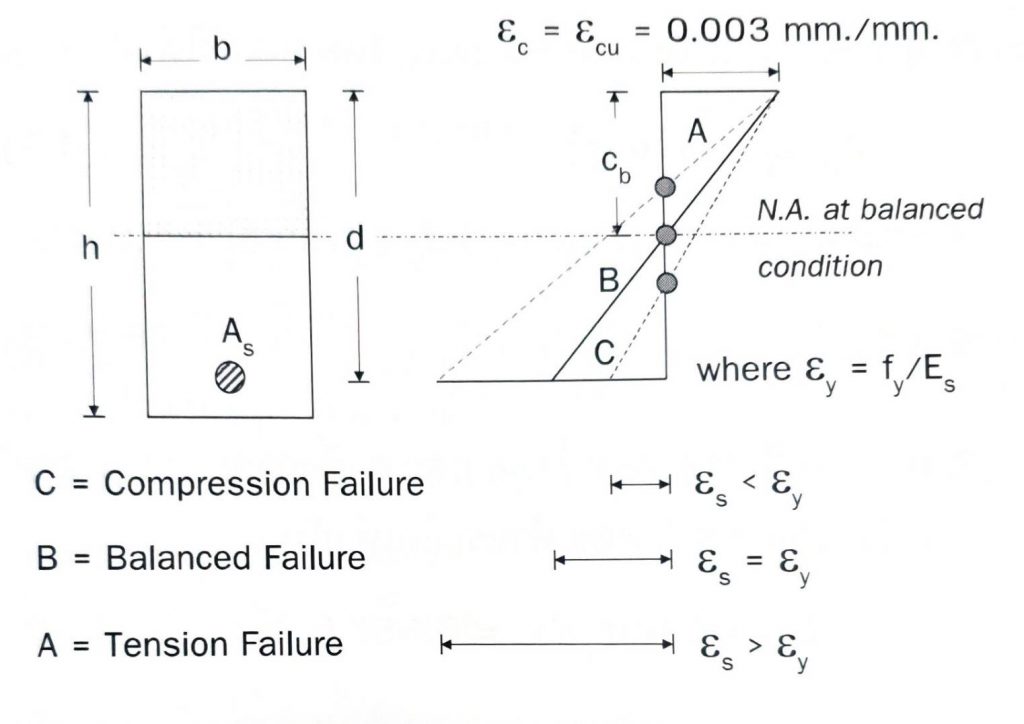
รูปที่ 5 ความสัมพันธ์ของ Strain ต่อความสูงหน้าตัดคานของแต่ละ mode การวิบัติ