การคำนวณหาปริมาณเหล็กเสริมและโมเมนต์ที่จุดสมดุล

ACI318 ให้การกระจายหน่วยแรงอัดในคอนกรีตที่ไม่เป็นเชิงเส้นเป็นเชิงเส้นในรูปของ หน่วยแรงเทียบเท่าสี่เหลี่ยมผืนผ้า (Rectangular Stress Block) ซึ่งมีค่าเท่ากับ $0.85f’_c$ ตลอดความลึก $a$ แทนการกระจายของหน่วยแรงที่เกิดขึ้นจริง โดยที่ $a = \beta_1c$ ดังแสดงในรูปที่ 6

โดยที่

แต่ทั้งนี้ $\beta_1$ ต้องมีค่าไม่ต่ำว่า 0.65

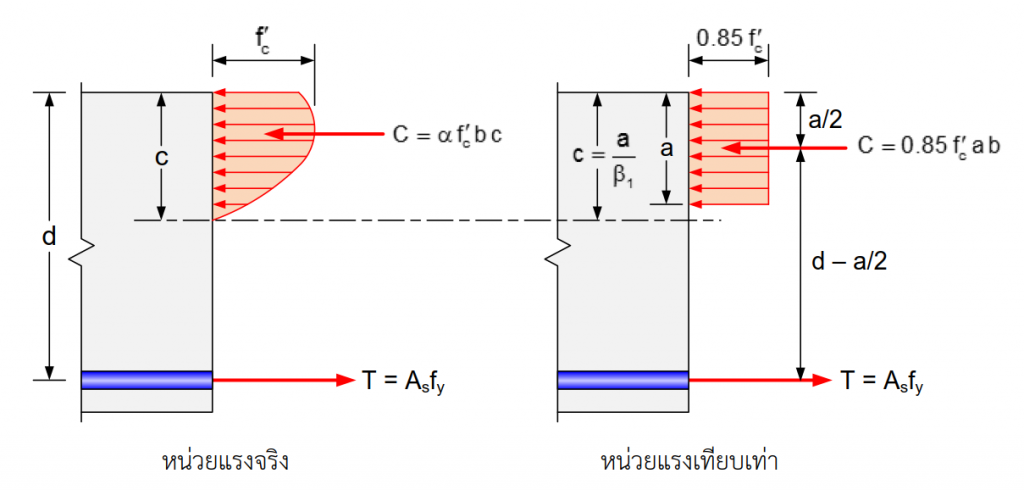
รูปที่ 6 ประมาณหน่วยแรงอัดไม่เชิงเส้นเป็นเชิงเส้น

การวิบัติที่จุดสมดุลก็คือ การวิบัติขณะที่ค่าความเครียดของคอนกรีตและเหล็กเสริมถึงจุดสูดพร้อมกันพอดี

นั่นคือ $\varepsilon_c = \varepsilon_{cu} = 0.003 mm./mm.$ และ $\varepsilon_s = \varepsilon_y$ ในเวลาเดียวกันพอดี ซึ่งจะได้หน้าตากราฟดังนี้

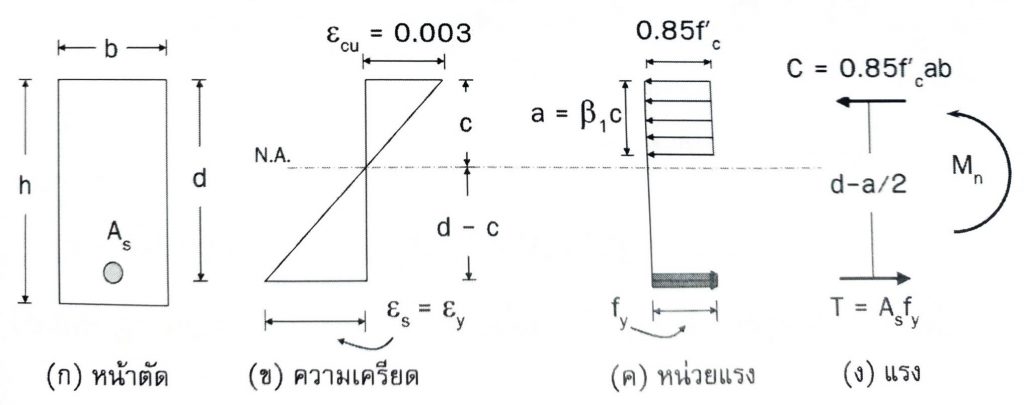
รูปที่ 7 กราฟ ความเครียด หน่วยแรง และแรง ของหน้าตัด

จากรูปที่ 7 (ข) จะได้สมการสามเหลี่ยมคล้ายดังนี้

$\varepsilon_{cu}/\varepsilon_y = c/(d-c)$ ….. (1)

แทน $\varepsilon_{cu} = 0.003$ และ $\varepsilon_y = f_y/E_s$ เมื่อ $E_s = 2.04×10^6 ksc$ จะได้

$c = (\frac{6120}{6120+f_y})d$ ….. (2)

จากความสัมพันธ์ของการกระจายตัวของแรงอัดและแรงอัดในรูปที่ 7(ค) และ (ง) จะได้สมการดังนี้

$C=0.85f’_cab = 0.85f’_c\beta_1cb$ ….. (3)

ในขณะที่แรงดึงในเหล็กเสริมเท่ากับ

$T = A_sf_y$ ….. (4)

จากสมดุลของหน้าตัด แรงอัดเท่ากับแรงดึง จะได้

$C = T$

$0.85f’_c\beta_1cb = A_sf_y$

จัดรูปใหม่ จะได้

$c = A_sf_y/(0.85f’_c\beta_1b)$ ….. (5)

เมื่อนำ $d$ หารตลอดสมการที่ (5) จะได้

$c/d = A_sf_y/(0.85f’_c\beta_1bd)$

เมื่อ $\rho = A_s/(bd)$ จะจัดรูปสมการใหม่ได้ว่า

$c/d = \rho[f_y/(0.85\beta_1f’_c)]$ ….(6)

แทนค่าสมการที่ (2) ลงในสมการที่ (6) จะได้อัตราส่วนเหล็กเสริมที่ภาวะสมดุล (balanced reinforcing ratio)

$\rho = \frac{0.85f’_c}{f_y}\beta_1(\frac{6120}{6120+f_y})$ ….. (7a)

เนื่องจากการวิบัตินี้ คือ ณ ตอนที่คอนกรีตวิบัติพร้อมกับเหล็กเสริมถึงจุดครากพอดี จึงห้อยท้ายพารามิเตอร์ต่าง ๆ ที่สภาวะนี้ด้วย $b$ เช่น $c_b, a_b, A_{sb}$ หรือ $\rho_b$ นั่นเอง ซึ่งจะทำให้สมการอัตราส่วนเหล็กเสริมที่ภาวะสมดุลดังนี้

$\rho_b = \frac{0.85f’_c}{f_y}\beta_1(\frac{6120}{6120+f_y})$ ….. (7b)

ซึ่งนอกจากนี้มีการทดลองและเสนอสมการอย่างง่ายในการคำนวณอัตราเสริมเหล็กที่ภาวะสมดุลไว้ดังนี้

$\rho_b =0.456(f’_c/f_y)$ ….. (7c)

สำหรับการหาโมเมนต์ก็ใช้หลักการของ โมเมนต์$=$ แรง $\times$ แขนตั้งฉาก ซึ่งสามาถหาได้จาก 2 ทางได้แก่ จากแรงอัด หรือ จากแรงดึง

• กรณีคิดโมเมนต์รอบแนวแรงดึง

$M_nb = C(d-a_b/2)$
$= 0.85f’_c\beta_1c_bb(d-\beta_1cb/2)$ ….. (8)

• กรณีคิดโมเมนต์รอบแนวแรงอัด

$M_nb = T(d-a_b/2)$

$= A_{sb}f_y(d-\beta_1c_b/2)$ ….. (9)

แต่ทั้งนี้ เพื่อไม่ให้คานวิบัติแบบเปราะ มาตรฐาน ACI จึงไม่นิยมให้เสริมเหล็กเกินอัตราส่วน $\rho_b หรือหากเกินก็ต้องปรับค่าตัวคูณลดกำลัง (Strength Reduction Factor, $\phi$) ให้โครงสร้างปลอดภัยมากยิ่งขึ้น โดย Code ACI แต่ละปีจะกำหนดค่าดังกล่าวไม่เท่ากัน

แต่ที่คนไทยคุ้นเคยที่สุดจะเป็น ACI318-99 ที่กำหนดให้อัตราส่วนเหล็กเสริมไม่เกิน 75% ของอัตราส่วนเหล็กเสริมที่ภาวะสมดุล

$\rho \leq 0.75\rho_b$