การออกแบบวิธีกำลัง (Strength Design Method, SDM)
การออกแบบวิธีกำลัง (Strength Design Method, SDM) หรือในช่วงปี ค.ศ. 1956-1970 จะถูกเรียกว่า วิธีกำลังประลัย (Ultimate Strength Design Method, USM) นั่น มีหลักในการพิจารณาความปลอดภัยของโครงสร้าง ณ สถาณะจำกัดประลัย (Ultimate Limit State) หรือสถานะที่ปริ่มขอบจะพังแล้ว
โดยตามแนวทางของ ACI318 (ซึ่งเป็นต้นแบบมาตรฐานของไทย) ได้กำหนดหลักการออกแบบไว้ดังสมการ ที่ (1)
$\phi M_n \geq M_u$ ….. (1)
โดยที่
$M_n$ คือ กำลังระบุเชิงดัด (Flexural Nominal Strength) หรือกำลังที่ควรรับได้ตามทฤษฎี
$\phi$ คือ ตัวคูณลดกำลัง (Strength Reduction Factor) หรือตัวคูณเพื่อลดกำลังการรับแรงจากทฤษฎี
$\phi M_n$ คือ กำลังดัดออกแบบ (Flexural Design Strength) หรือกำลังรับแรงดัดที่ออกแบบไว้ให้ใช้งานได้ไม่เกินค่านี้
$M_u$ คือ โมเมนต์ออกแบบประลัย (Ultimate Design Moment) หรือแรงดัดประลัยที่ใช้สำหรับออกแบบ
ทั้งนี้ $M_n$ นั่นไม่ได้เป็นโมเมนต์ที่หน้าตัดจะเกิดการวิบัติจริง แต่เป็นโมเมนต์ที่คาดว่าจะเป็นเป็นโมเมนต์วิบัติของหน้าตัด
ส่วน $M_u$ นั่นเกิดจากการขยายค่าโมเมนต์ที่คาดว่าจะเกิดขึ้นด้วยตัวคูณที่เรียกว่า ตัวคูณกำลัง (Load Factor) เพื่อจำลองน้ำหนักบรรทุกที่คาดว่าอาจเป็นตัวที่ทำให้โครงสร้างเกิดการวิบัติเพื่อใช้ในการออกแบบ ตามแสดงในสมการที่ (2)
$M_u = \gamma_DM_D + \gamma_LM_L$ ….. (2)
โดยที่ $\gamma_D$ คือตัวคูณกำลัง (Load Factor) สำหรับโมเมนต์ที่เกิดจากน้ำหนักบรรทุกคงที่ (รวมถึงน้ำหนักตัวเอง)
และ $\gamma_L$ คือตัวคูณกำลัง (Load Factor) สำหรับโมเมนต์ที่เกิดจากน้ำหนักบรรทุกจร
สำหรับค่าของ $\gamma_D$ และ $\gamma_L$ นั่นแต่ละมาตรฐานจะมีค่าที่แตกต่างกัน ดังนี้
| มาตรฐาน | Load Factor for DL ($\gamma_D$) | Load Factor for LL ($\gamma_L$) |
| กฎกระทรวงฉบับที่ 6 (พ.ศ. 2527) | 1.7 | 2.0 |
| วสท.1008-38 (EIT 1008-38) | 1.4 | 1.7 |
| ACI318-99 | 1.4 | 1.7 |
| ACI318-08/11/14/19 | 1.2 | 1.6 |
สำหรับค่าของตัวคูณลดกำลังสำหรับแรงดัด ($\phi$) นั่นก็แตกต่างไปตามมาตรฐานเช่นกัน ดังนี้
| มาตรฐาน | ตัวคูณลดกำลังสำหรับแรงดัด (Strength Reduction Factor , $\phi$ ) |
| กฎกระทรวงฉบับที่ 6 (พ.ศ. 2527) | ไม่ได้กำหนด |
| วสท.1008-38 (EIT 1008-38) | 0.9 สำหรับงานที่ควบคุมคุณภาพ 0.8 สำหรับงานที่ไม่มีการควบคุมคุณภาพ |
| ACI318-99 | 0.9 |
| ACI318-08/11/14/19 | แปรผันตาม $\varepsilon_t$ |
ค่า $\varepsilon_t$ คือ Tension strain at extreme layer หรือค่าความเครียดที่เหล็กชั้นนอกสุดของหน้าตัด
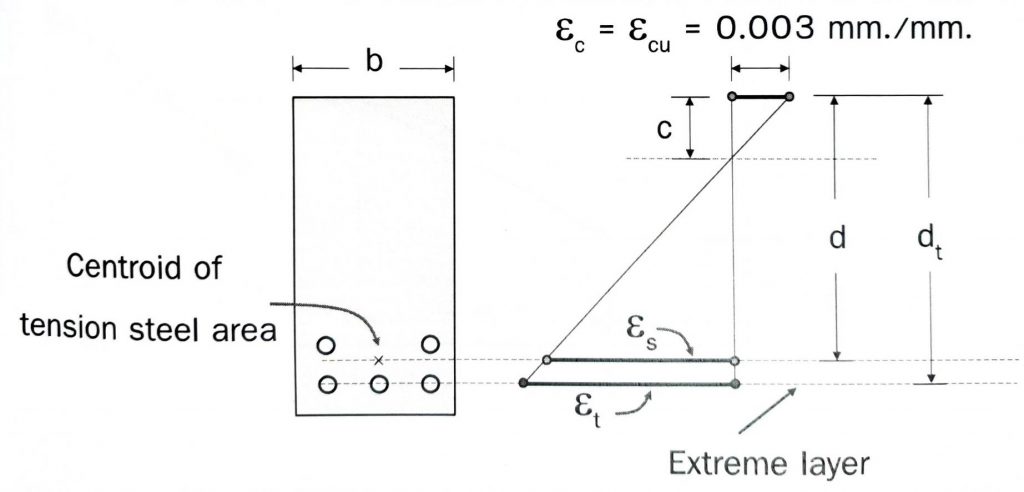
รูปที่ 1 ความหมายของ $\varepsilon_t$