*** บทความนี้ใช้หน่วย ksc

พื้นฐานแรงเฉือน

ในบทความนี้ ขอข้ามทฤษฎีพื้นฐานเกี่ยวกับแรงเฉือน เนื่องจากไม่ต่างจากตำราที่หาอ่านได้ทั่วไป และเพื่อเข้าเนื้อหาสมการการคำนวณและเปรียบเทียบมาตรฐานต่าง ๆ อย่างรวบรัดทีสุด

คานวิบัติแบบเฉือนแยกเป็น 2 รูปแบบหลัก ๆ ได้แก่ Shear-compression และ Inclined crack

โดยจะวิบัติรูปแบบไหนขึ้นอยู่กับอัตราส่วน a/d ของคาน

Shear-Compression จะเกิดขึ้นเมื่อค่า a/d < 2.0-2.5 ซึ่งก็คือคานสั้นหรือคานลึก
Inclined crack จะเกิดขึ้นเมื่อค่า a/d > 2.0-2.5 ซึ่งก็คือ คานยาว
แต่หาก a/d = 0 จะเป็นเสา Pure Axial

โดยที่
a = ระยะห่างระหว่างแรงกระทำกับ Support
d = ความลึกประสิทธิผล

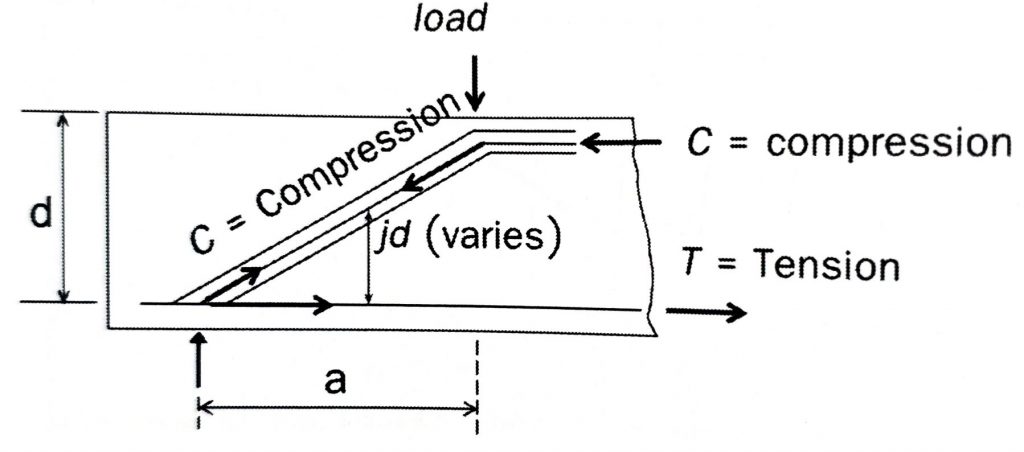
รูปที่ 1 พฤติกรรม Arch action ในคานคอนกรีตบริเวณ Support

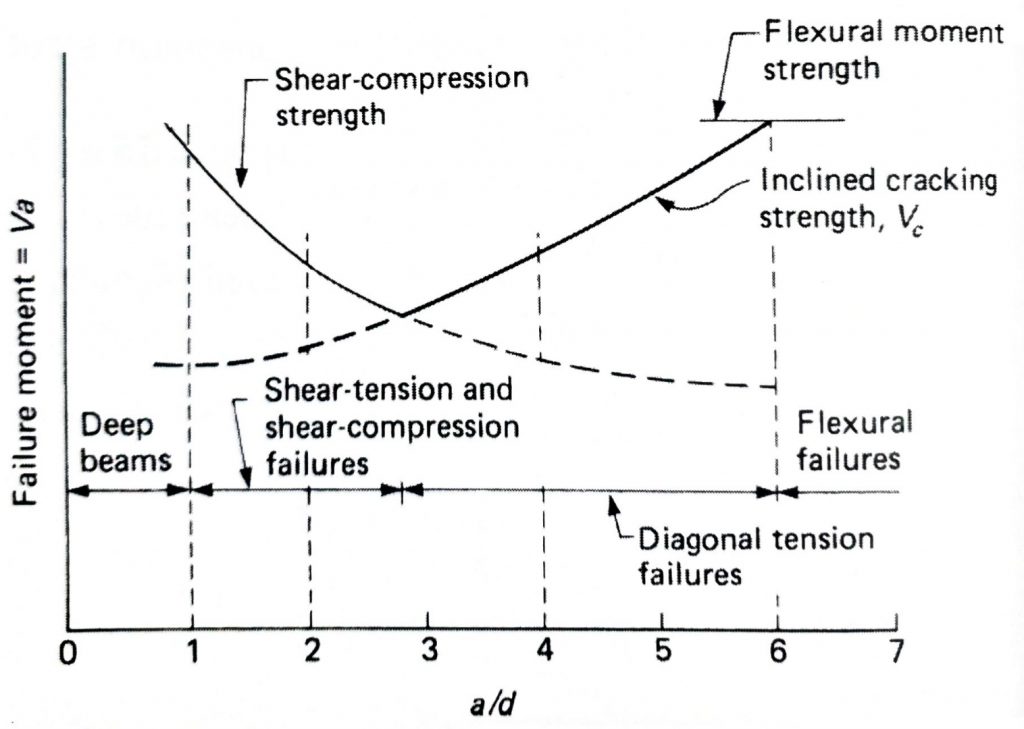
รูปที่ 2 อิทธิพลของ a/d ต่อรูปแบบการวิบัติของคานเนื่องด้วยแรงเฉือน

โดยในบทความต่อไปนี้ จะพูดถึงเฉพาะคานยาวที่วิบัติโดย Inclines cracking เท่านั้น

กลไกการต้านทานแรงเฉือนในคานที่ไม่เสริมเหล็กปลอก

พฤติกรรมคานรับแรงเฉือนไม่ใส่เหล็กลูกตั้ง

การต้านแทนแรงเฉือนของคานไร้เหล็กปลอกพฤติกรรมเป็นไปตามรูปที่ 3

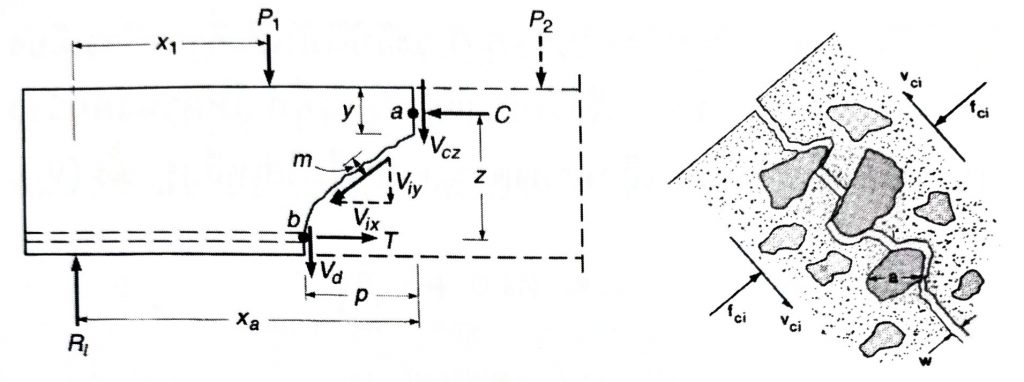
รูปที่ 3 กลไกต้านทานแรงเฉือนของคอนกรีตในคาน คสล.

โดยที่
$V_{cZ}$ = ความต้านทานแรงเฉือนของหน้าตัดคอนกรีตไม่แตกร้าว
$V_{ix}$ และ $V_{iy}$ = ความต้านทานแรงเฉือนของมวลรวมในแนวสัมผัสกับรอยร้าว คล้ายกับแรงเสียดทานระหว่างผิวคอนกรีตในแต่ละด้านของรอยร้าว
$V_d$ = ความต้านทานของเหล็กเสริมหลักต่อแรงเฉือน

เมื่อ $V_c = V_{cZ} + V_{iy} + V_d$
โดยที่ $V_c$ คือกำลังต้านทานแรงเฉือนโดยคอนกรีต

สำหรับคานที่มีค่า a/d ระหว่าง 2.5-6.0 จะวิบัติทันทีเมื่อรอยร้าวเอียงเกิดขึ้น ดังนั้น ACI318 จึงถือให้แรงเฉือนที่ทำให้คานแตกร้าว (Inclined cracking) เป็นกำลังรับแรงเฉือนของคานที่ไม่ใส่เหล็กปลอก ($V_c$)

จากการทดลองจะได้กำลังรับแรงเฉือนของคานเป็นไปตามรูปที่ 4 ACI จึงเสนอสมการกำลังต้านทานแรงเฉือนของคอนกรีตดังนี้

$V_c = (0.50\lambda(f’_c)^{0.5} + 176\rho_w(V_ud/M_u))b_wd \leq 0.93(f’_c)^{0.5}b_wd$ ….. (1)

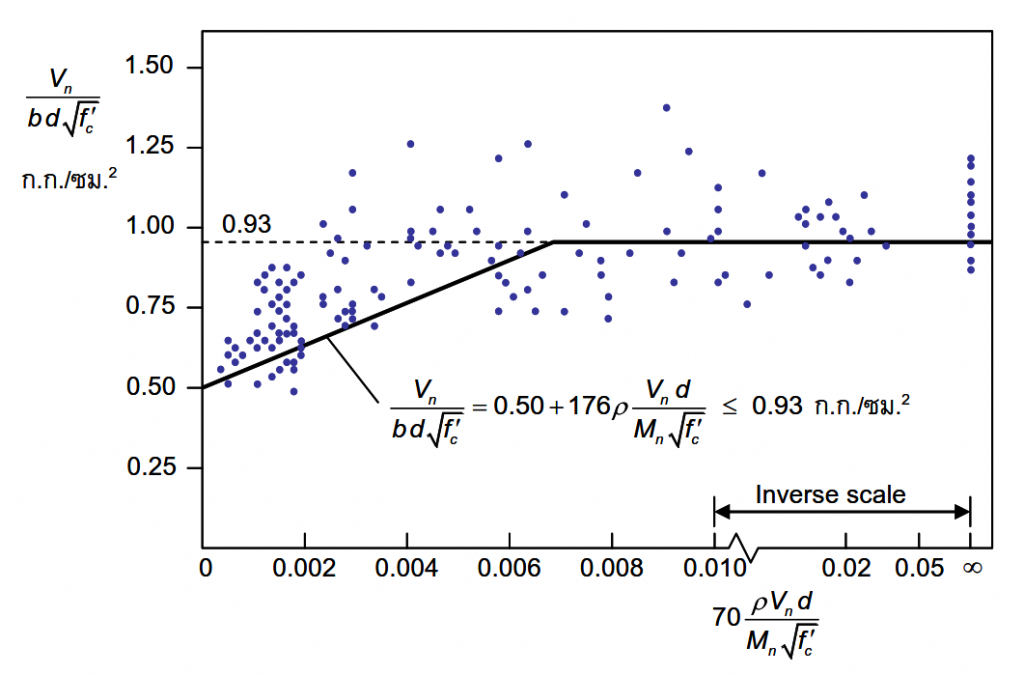
รูปที่ 4 กราฟผลการทดลองกำลังรับน้ำหนักของคานไม่เสริมเหล็กปลอก

แต่เนื่องจากการคำนวณที่ยุ่งยาก ทำให้คำนวณมือไม่สะดวก ประกอบกับค่า $\rho_w, V_u, M_u$ มีค่าไม่คงที่ตลอดหน้าตัด ACI318 จึงยอมให้ใช้สูตรที่ง่ายกว่า คือ

$V_c =0.53(f’_c)^{0.5}b_wd$ ….. (2)